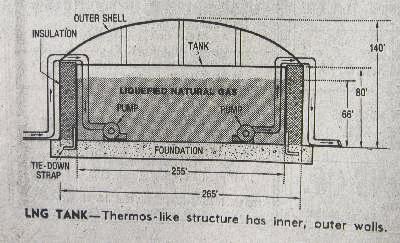

This study deals with heat flowing to the tank submerged in the ground. The underlying problem relates to storing large volumes of liquefied natural gas (LNG) at -259 degrees Fahrenheit. The objectives are to find the freezing line of the ground, look at the heat flow through a single point, and consider the effects of the tank on it's surrounding.
To store LNG, a commercial design, based on experimental verification of its feasibility, contemplated a prestressed concrete tank 255 feet in diameter and 80 feet deep that would hold 600,000-bbl of liquefied gas at -259 degrees Fahrenheit. The boiling point of LNG is -258 degrees F, so with refrigeration continually converting the vapors to liquid, the temperature will remain uniform at this value.
A container of that size, with a temperature that cold, will have effects on everything around it. Important considerations of the design are the rate of heat gained from the surroundings (which causes evaporation of the liquid gas) and variation of temperatures in the earth below the tank. The safety of the tank could be affected by possible settling or frost-heaving.
In this study, one-dimensional heat flow under the center of the tank is considered. Some questions to be answered are how far away is the ground not affected by the heat flow, and what is the heat flow through a single point close to the tank?
The basic mathematical model for unsteady-state flow is the following
parabolic partial-differential equation.
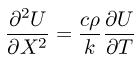
Where c is the heat capacity or specific heat, ρ is the density, and k is the thermal conductivity. Applied Numerical Analysis by Gerald and Wheatley published by Addison Wesley was used as a reference. Using a finite-difference approximation we can use the following equation.
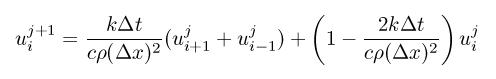
The subscript denotes the position and the superscript denotes time. The equation is solved for temperature at each point uij+1 in terms of the temperatures at time tj. This is coded in Fortran.
The output from running the code shows the temperature of first fifty feet away from the bottom of the tank after ten and a half days. At twelve feet below the tank, the temperature is 32.24 degrees Fahrenheit. This is where there would be a change between frozen ground and just cold ground.
Many questions are still unanswered by this study that would be interesting to look into. What affect does that large amount of cold material have on the climate around it? If much cold was transmitted to the air, would rain turn into hail around the tank? Would animals avoid getting close to it because of the cold? What if the ground was wetter or dryer? Would there be any difference if the daytime and nighttime temperature difference were considered?