The Physics Teacher
November 1993
Volume 31/Number 8
The Physics of Bungee Jumping
Paul G. Menz
The
vocabulary is new and multisyllabic - slingshotting, sandbagging, bodydipping,
vinejumping, part-of-four, and more. The spelling is erratic - bungee, bungi,
bungy. And terra firma types would say the trendy activity is a threat to body
wholeness. But physicists, of course, calmly regard bungee jumping as a
dramatic demonstration of the conversation of energy. They know that
gravitational potential energy at the top of the jump is converted to elastic
potential energy at the bottom. The basic equations involved have been used for
years to describe events in which loads are suddenly applied to springs. The
bungee cord is simply a very weak spring yielding large spring deflections and
rather small force magnitudes. But for the benefit of those who didn't know
this, we'll lay it all out here.
History
The
origin of sport bungee jumping is quite recent, but the activity is related to
the centuries-old ritualistic practices of "land divers" of Pentecost
Island in the Pacific Archipelago of Vanuatu. There the men demonstrate their
courage and offer their injuries to the gods for a plentiful harvest of yams.
But it was members of the Oxford University Dangerous Sport Club who, inspired
by a film about "vine jumpers," plummeted off a bridge near Bristol,
England, in April 1979 and thereby launched a new worldwide recreational
activity. During the 1980s, the sport flourished in New Zealand and France and
was brought into the United States by John and Peter Kockelman of California.
In the early 1990s facilities sprang up all over this country with cranes,
towers, and hot-air balloons serving as platforms. Thousands have now
experienced that "ultimate adrenaline rush." Many have tried to
describe that exhilaration. All share the post-jump elation and grin. In Fig. 1
the jumper, following countdown, has leapt backwards. In Fig. 2, the jumper is
enjoying that motionless instant at the top of the rebound.
Equipment
Bungee
cords have some vague military origin, but today can be purchased from
manufacturers who construct them specifically for jumping. They are soft and
springy and may stretch to three or four times their free length. The harnesses
are related to and derive from mountain climbing equipment, as does the
carabiner, which is the principal link between the cord and the harness. Most
present-day facilities use redundant connections, that is, double hookups to
the jumper's body are provided as shown in Figs. 3 and 4. If a jumper chooses
an ankle jump, the body harness is backup; if the body harness is primary, the
chest/shoulder harness is secondary.
Safety
This
article is not a commercial for bungee jumping, but familiarity with the
equipment used and the forces involved may surprise some readers and may
testify to the safety of this activity as a sport. The activity was banned in
France after three deaths in 1989. The Australian government declared a hiatus
after an accident in 1990, and the summer of 1992 saw a few accidents in the
United States that were given major exposure by the media and caused several
state governments to get involved. But the activity is clearly basically safe.
All accidents can be traced to human error as related to improper attachment,
mismatch between jumper and cord, total height of jump available,
misunderstanding or miscalculation of the physics involved, and other lapses.
This view is shared by Carl Finocchiaro, a registered professional engineer who
operates Sky Tower Engineering Inc. and has been professionally involved in
this sport for several years. He is a charter member of the North American
Bungee Association and is the original and incumbent chairman of its safety
committee. He has stated, "I have investigated many accidents and can
confidently conclude that all are caused by human error and not faulty
equipment."
Minor
injuries such as skin burn, which is caused by gripping the cord, occur when
jumpers act contrary to instructions. Some jumpers reported getting slapped in
the face by the cord. But serious injury inflicted by the cord, such as
strangulation, appears not to happen. This can be explained by a combination of
factors, including:
- the cord's minimal torsional stiffness
- some pendulum motion, which tends to keep the cord away from the
jumper
- the fact that any entanglement will occur when the cord is slack,
and will be gradually and gently unwrapped and forgiven as the cord
develops elongation and associated low tensile force.
No modern-day jump site has
seen any serious entanglement, and it is noteworthy that many participants
enjoy somersaulting during the free fall without any detrimental effects.
Some
daredevilish embellishments may tempt the adventurous participants.
"Slingshotting" (from the ground up), "sandbagging"
(jumping with extra weight), and "bodydipping" (over water) are
examples. Extreme care and proper application of the physics involved are
vitally important in these challenges.
Physics of Bungee Jumping
The
principle components in the physics of this sport are the gravitational
potential energy of the jumper and the elastic potential of the stretched cord.
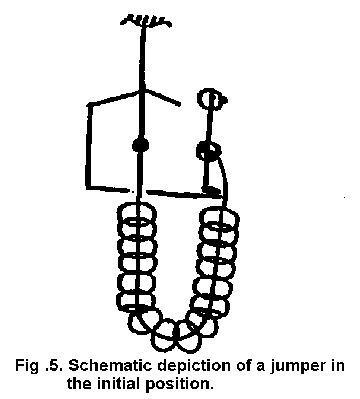
Figure
5 depicts a jumper of mass m who is tethered by a bungee cord conveniently
attached to the supporting structure on a level with her center of mass.
Figure
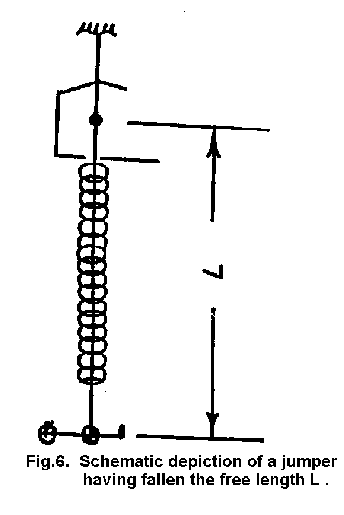
6 depicts the jumper just as she has fallen a distance equal to the free length
(L) of the cord. This event terminates the free fall, which lasts between one
and two seconds.
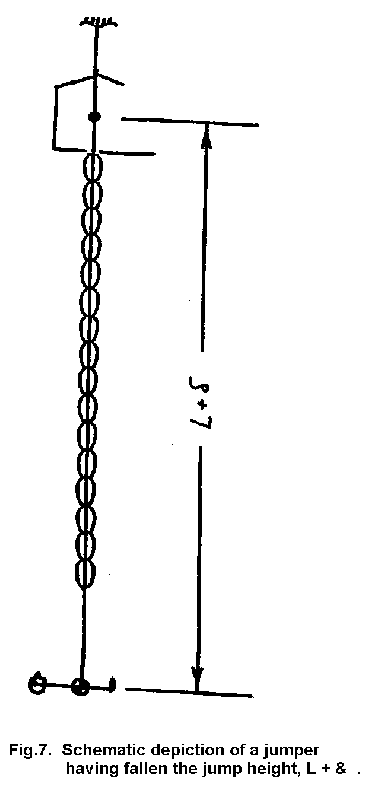
Figure
7 depicts the jumper at the bottom extremity of the jump. The jumper has fallen
a total distance of L + d, the cord has stretched a distance d, and the
velocity of everything at that instant is equal to zero.
Energy
considerations dictate that the gravitational potential energy of the jumper in
the initial state is equal to the elastic potential of the cord in the final
state. Therefore:
![]()
If
we allow the bungee cord to be a linear spring of stiffness K N/m, then
![]()
and
from this the following quadratic equation is produced:
![]()
When
a given cord (K,L) is matched with a given person (m), then the d will be
determined by
When a given jump height (L
+ d) is to be matched with a given person (m), then the stiffness (K) will be
determined by
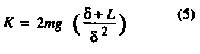
In
many cases, the first match is made so that the total fall (L + d) will fit the
facility, but in order to show the orders of magnitude involved, consider a
hypothetical second match between a person (m) and a jump height (L + d).
Suppose a person weighing 667 N is to jump using a 9-m cord which will stretch
18 m and use a jump height of 27 m:
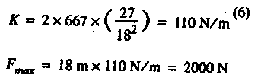
This
200% elongation produces a maximum force three times the jumper's weight. A
300% elongation is a softer ride:
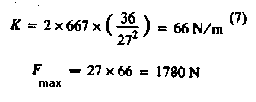
This
requires a jump height of 36 m, and a maximum acceleration of 2.7 g's is
produced.
Calculations Closer to Reality
In
a more realistic vein, two factors must be considered:
- A given facility will have a limited number of cords of differing
lengths and stiffnesses.
- Those cords have been found to demonstrate variable stiffness over
their range of use.
Some actual force-deflection
diagrams are shown in Fig. 8,
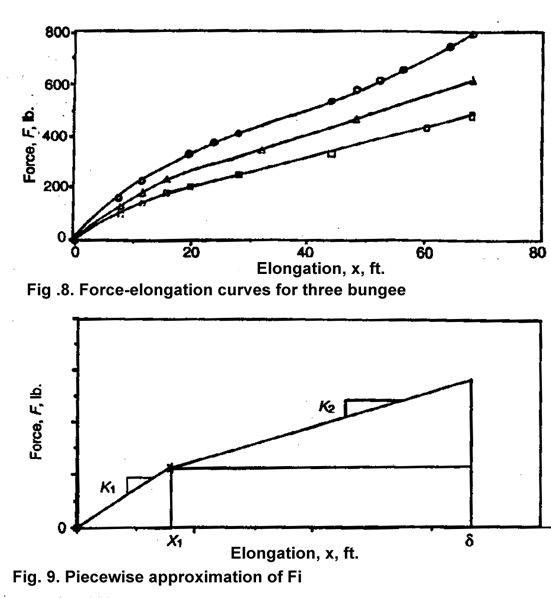
and
a piece wise linear approximation is shown in Fig. 9. Three areas are
delineated in Fig. 9 so that Fdx can be evaluated as a sum of areas:
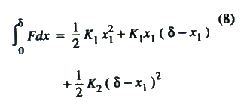
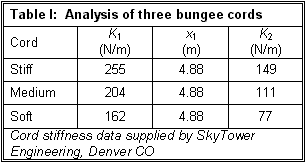
Analysis
of these three bungee cords yields the information found in Table I.
A third factor, which
complicates the arithmetic but contributes in two ways to a facility's
improvement, is the addition of a static line (see Fig. 10).
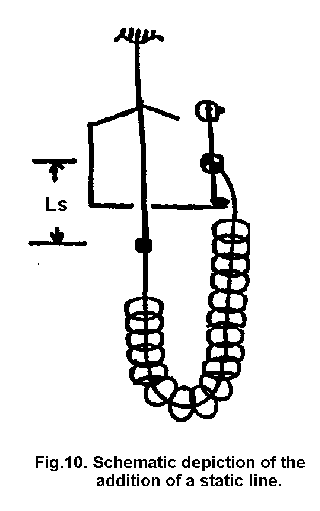
This
rigid line or cable prevents the cord itself from rubbing or chafing against
the floor of the basket or tower. It also may be played in or out to customize
the jump height to any individual. The conservation of energy then takes this
form:
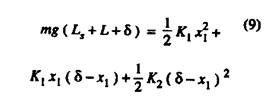
which
yields the following quadratic equation:
It
seems plausible to match a heavy person (1112 N) with the stiff cord, a medium
person (800 N) with the medium cord, and the soft cord with a jumper of about
490 N. The calculations have been performed using a free length (L) of 9 m, a
static cable length (Ls) of 1.8 m, and the matched jumpers and cords. The
results are presented in Table II, which shows the maximum forces and the
number of g's obtainable from Eqs. (9) and (10) respectively
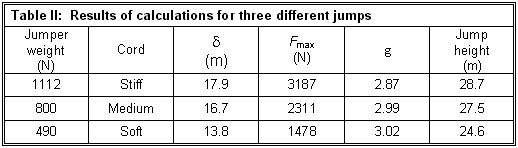
Some
organizations might give the light jumper a 27- to 28-m ride to match the
geometry of a given tower or crane. This can be done by adding length to the
static line. Suppose Ls is increased to 3.6 m for the 490-N jumper. Then d =
14.5 m, the jump height increases to 26.8 m, and the g value becomes 3.13.
Discussion
We
see from both the hypothetical linear spring and the real nonlinear spring that
the proper match of cord and jumper should produce maximum accelerations of the
order of 3 g's, and with a cord of about 9 m free length, the jump height
should be approximately 28 m.
The
material presented here offers the instructor of introductory physics an
"in-vogue" application of the conservation of energy concept that is
related to both entertainment and athleticism. Also, perhaps a teacher could
devise an appealing laboratory exercise using the same applications for short
bungee cords (0.6 m or so) and masses from the stockroom (with due attention
being given to the masses as they rebound!).
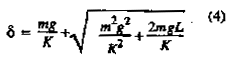
Finally,
it is informative to consider Eq. (4) carefully because it depicts one of the
most important practical ideas to be learned from dynamics, whether or not it
is related to bungee jumping. Equation (4) is applicable to any weight mg being
dropped onto a compression spring of stiffness K from distance L above. Even if
dropped from a distance of L=0, the mass creates a d of 2 mg/K; which is
exactly twice the effect realized if the mass is applied gradually. In other
words, if a load is administered to any system or structure suddenly or
dynamically, the force imposed is, at the minimum, twice as great as the static
load.
References
- David Thigpen, Time, April 23, 1990, p. 75.
- Jeremy Hart, World, May, 1991, pp. 40-45.
- Carl Finocchiaro, Sky Tower Engineering, Inc., 1340 Dahlia Street,
Denver, CO 80220, "Engineering Report," March 3, 1992.
- 4. F.W. Sears and M.W. Zemansky, University Physics, 3rd ed.
(Addison-Wesley, Reading, MA, 1963), p. 174.